Adição de arcos
Cosseno da soma
Considere a figura ao lado. Sejam três pontos 
 e
e  pertencentes à circunferência , cujas coordenadas são
pertencentes à circunferência , cujas coordenadas são 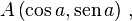
 e
e 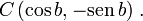 Os arcos
Os arcos 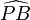 e
e  têm medidas iguais, logo as cordas
têm medidas iguais, logo as cordas  e
e 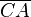 também têm a mesma medida. Após aplicarmos a fórmula da distância entre dois pontos da Geometria analítica, temos:
também têm a mesma medida. Após aplicarmos a fórmula da distância entre dois pontos da Geometria analítica, temos:


Ao igualarmos as duas expressões, temos a fórmula:
Seno da soma
Sabemos que  A partir disto e sendo
A partir disto e sendo 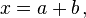 obtemos:
obtemos:
Utilizando a fórmula do cosseno da diferença de dois arcos nessa última expressão:
Substituindo  e
e  nesta expressão, então:
nesta expressão, então:
Tangente da soma
Sabendo que  e utilizando as fórmulas anteriores para soma de senos e cossenos, podemos facilmente conseguir uma expressão para
e utilizando as fórmulas anteriores para soma de senos e cossenos, podemos facilmente conseguir uma expressão para 

Então:
Vale lembrar que essa fórmula só pode ser usada se  e
e  porque a relação
porque a relação  só é válida se e somente se
só é válida se e somente se 
Cotangente da soma
Como  podemos obter, de maneira semelhante à formula da tangente da soma, uma expressão para
podemos obter, de maneira semelhante à formula da tangente da soma, uma expressão para 

Simplificando, temos:
Como  é válida se e somente se
é válida se e somente se  a identidade que demonstramos acima só pode ser usada se
a identidade que demonstramos acima só pode ser usada se  e
e 
Exemplos
- Calcule:
-
- Resolução


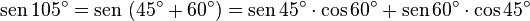







Subtração de arcos
Cosseno da diferença
Para calcular  fazemos uso da igualdade
fazemos uso da igualdade  na fórmula do cosseno da soma, conforme a seguir:
na fórmula do cosseno da soma, conforme a seguir:


Então:
Seno da diferença
Podemos fazer a mesma substituição da igualdade  para encontrar as outras relações de diferença de arcos. Para o seno, usaremos a fórmula do seno da soma e a igualdade citada acima, conforme a seguir:
para encontrar as outras relações de diferença de arcos. Para o seno, usaremos a fórmula do seno da soma e a igualdade citada acima, conforme a seguir:
Logo,
Tangente da diferença
Usando novamente a igualdade  e, desta vez, a fórmula da tangente da soma:
e, desta vez, a fórmula da tangente da soma:
Simplificando, temos:
Pelos motivos já citados anteriormente, esta fórmula só é válida se  e
e 
Cotangente da diferença
Mais uma vez, usaremos a igualdade  e, desta vez, a fórmula da cotangente da soma:
e, desta vez, a fórmula da cotangente da soma:
Logo, obtemos a identidade:
Está fórmula só pode ser aplicada se  e
e 
Exemplos
- Calcule:
-
- Resolução









- Dados
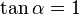 e
e  calcule
calcule 
-
- Resolução


Multiplicação de arcos
É possível deduzir fórmulas para calcular as funções trigonométricas de 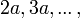 utilizando as fórmulas obtidas para a soma de arcos e fazendo
utilizando as fórmulas obtidas para a soma de arcos e fazendo 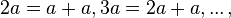 conforme será mostrado adiante.
conforme será mostrado adiante.
Cosseno
Usando a fórmula do cosseno da soma, temos:
Logo, utilizando a Identidade relacional básica, podemos obter duas fórmulas finais:
ou



Utilizando a Identidade relacional básica e trabalhando algebricamente, temos:
Expressões para  são obtidas por processos semelhantes.
são obtidas por processos semelhantes.
Seno
Ultilizando a fórmula do seno da soma:
Então, temos:
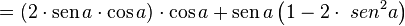
Utilizando a Identidade relacional básica:
Logo:
Expressões para  são obtidas por processos semelhantes.
são obtidas por processos semelhantes.
Tangente
A partir da fórmula da tangente da soma:
Logo:
Ao subtituimos a fórmula anterior para 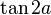 e simplificarmos, obtemos como fórmula final:
e simplificarmos, obtemos como fórmula final:
Expressões para  são obtidas por processos semelhantes.
são obtidas por processos semelhantes.
Exemplo
- Se
 e
e  calcule
calcule 
-
- Resolução
Precisamos encontrar  para aplicarmos a fórmula. Para tanto, utilizaremos a identidade
para aplicarmos a fórmula. Para tanto, utilizaremos a identidade 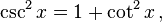 que relaciona as funções cotangente e cossecante. A partir da cossecante obtida, podemos encontrar o valor do seno, uma vez que
que relaciona as funções cotangente e cossecante. A partir da cossecante obtida, podemos encontrar o valor do seno, uma vez que  Como
Como  o valor da cossecante é positivo.
o valor da cossecante é positivo.

De onde vem 
Podemos finalmente calcular:

Bissecção de arcos
Cosseno
Vamos utilizar as duas fórmulas que encontramos para  a fim de que, dado o cosseno de uma arco
a fim de que, dado o cosseno de uma arco  qualquer, possamos obter
qualquer, possamos obter  ou
ou  Para isto, consideraremos
Para isto, consideraremos 
A partir de 
A partir de  temos:
temos:
Finalmente, sabendo que  temos:
temos:
Seno
Caso nos seja dado o  sabendo que
sabendo que  calculamos
calculamos  e usamos as fórmulas dadas logo acima para o cosseno.
e usamos as fórmulas dadas logo acima para o cosseno.
Tangente
Precisamos agora encontrar fórmulas que permitam calcular 
 e
e 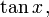 conhecida a
conhecida a  Para tanto, tomaremos as fórmulas de multiplicação
Para tanto, tomaremos as fórmulas de multiplicação


e consideraremos  de modo que:
de modo que:
Exemplos
- Se
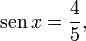 com
com  calcule as funções circulares de
calcule as funções circulares de 
-
- Resolução

Logo, temos:
- Se
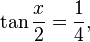 determine
determine 
-
- Resolução
Podemos aplicar diretamente a fórmula, de modo que:

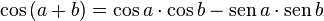
![\mathrm{sen}\, \left ( a + b \right ) = \cos \left [ \frac{\pi}{2} - \left ( a + b \right ) \right ] = \cos \left [ \left ( \frac{\pi}{2} - a \right ) - b \right ]](http://upload.wikimedia.org/math/6/f/e/6fe9329ba5e60e1289e0ce14f545cb3f.png)











![\cos \left ( a - b \right ) = \cos \left [ a + \left ( -b \right ) \right ] \;\!](http://upload.wikimedia.org/math/0/8/b/08bf8219fc6048c78623d4d7368053b4.png)
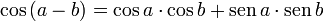
![\mathrm{sen}\, \left ( a - b \right ) = \mathrm{sen}\, \left [ a + \left ( -b \right ) \right ] = \mathrm{sen}\, a\cdot\cos \left ( -b \right ) + \mathrm{sen}\, \left ( -b \right )\cdot\cos a \;\!](http://upload.wikimedia.org/math/0/9/4/0948c83d3bd459b0a8321b2458b0f1b2.png)

![\tan \left ( a - b \right ) = \tan \left [ a + \left ( - b \right ) \right ] = \frac{\tan a + \tan \left ( -b \right )}{1 - \tan a\cdot\tan \left ( -b \right )}](http://upload.wikimedia.org/math/e/a/e/eae9162e77a213f16200443ee63301b9.png)

![\cot \left ( a - b \right ) = \cot \left [ a + \left ( -b \right ) \right ] = \frac{\cot a\cdot\cot \left ( -b \right ) - 1}{\cot a + \cot \left ( -b \right )}](http://upload.wikimedia.org/math/f/2/3/f238db03f70111c90309eddb92193cb8.png)





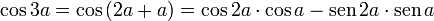




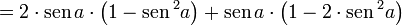



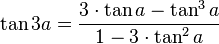

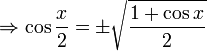











Nenhum comentário:
Postar um comentário